粉末X線回折測定(理論編)
粉末X線回折(XRD)法はセラミックス、金属材料の相同定から結晶構造解析には不可欠の手法だ。特に、単結晶が得られにくいセラミックス材料などでは、実験室設置型のXRD装置でも良質なデータが得られる。ここでは、粉末XRDの測定原理について、なるべく数式を使わないで、(というより数式を使えないおサルな)中山の理解しているところを書いていく。といっても、例によって勘違いなどはあると思うので、その辺は穏やかに指摘してください。
回折法から得られる情報1
粉末XRDから得られる情報は下の図に示すように幅広い。 が、よくよく考えてみると回折装置が測定して吐き出すデータというのは、サンプルとX線入射光がなす角と、そのときの回折強度の2つのデータしかない。 だから、2つのパラメーター「回折角と回折強度」がどういった原理で決定されるのかを考えればいいことになる。 ところで、最初は話を単純にするために、 1)試料は結晶で 2)不純相がなくて 3)格子のサイズや結晶子サイズの影響を受けない、そして4)基本的には入射X線は単色光(波長が一定)であるという条件を考えてみよう。図2に示したように、サンプルに一方向からX線を入射したときに、回折角2θに対してどれくらいの強度のX線ビームがやってくるかということである。


X線の散乱
まず1個の電子にX線が当たったときに起きる現象を考えてみる。 X線は電磁波だから、振動する電場の波と考えて差し支えない。で、その波が空間を伝わってきて、電子(荷電粒子)当たることを想像してみよう。当然、電子はX線の振動する電場に振り回されて、振動をはじめるのだ。そうすると、電子が振動されたことによって新たに電磁波が発生する。これが散乱である。そして、XRDではこの散乱波のみを考えて理論が構成されている。そのほかの理由で発生するX線は理論の範ちゅう外なので無視無視。(後述の★を参照) このとき、発生する散乱波は球面波で、入射X線が無偏光だったら全ての方向に均等に散乱波を広げていくようにも見えるのだが、特定の入射方向からビームに対する散乱ということで幾何学的な条件が入るため、偏光因子(あるいは偏極因子)というファクターが入って、2θに対して強度が変化する関数になる。
さて、ココでの話をまとめると、荷電粒子にX線がぶち当たると球面散乱波を発生するということがわかった。で、これが後で述べる回折現象のオオモトになっているわけだ。もうひとつ重要なことを述べておこう。物質を構成する荷電粒子には、電子だけではなくて陽子もある。でも、陽子(そしてその集合体である原子核)はトテモ重いので、入射X線の電場で強制振動させられてもあまり強い散乱波は出てこない。ということで、この陽子による散乱の寄与は無視できてしまう。
★散乱波以外で、装置のディテクターにやってくると思われるX線としては、(簡単に想像できるように)そもそも電子にぶつからなかった入射波(透過波)の割合が一番大きい。当然θ=0度付近で顕著だ。で、装置の回折系にもよるがその強度は散乱波に比べて著しくデカイため、不適当なディテクターを0度付近にセットしてX線を通すと、ディテクターが壊れてしまうので注意。
★上述した散乱波というのは、弾性散乱波(トムソン散乱波)である。これは入射波と散乱波のX線エネルギーが変化しない場合である。(X線のエネルギーとは散乱強度と違う。一フォトンあたりのエネルギー。つまりここでは、波長が変わらないことを言っている)。非弾性散乱(コンプトン散乱)は散乱時にエネルギーのやり取りがある場合で、初歩的な回折理論(つまりこのページ)ではその寄与を考えない。でも、非弾性散乱の効果を利用した異常分散法なんていうのもあるのでアドバンスなことをやっている人には重要。

複数の電子による散乱1(干渉効果)
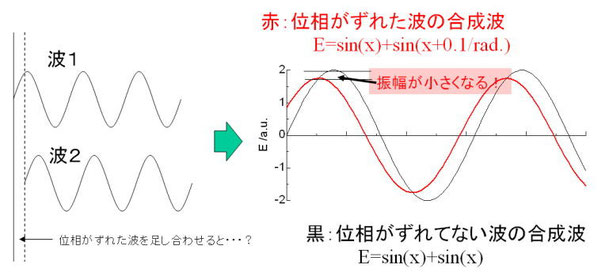
今度は、電子が複数ある場合の散乱現象について考えてみよう。たとえば、電子が10個あったら、散乱光の強度は10倍になるのではないのと考えたくなるのが(あまり深く物事を考えたくない人の)人情なのだが、残念ながらそうではない。(ちなみにθ=0では、この考え方は成り立つし、電子数が増えれば増えるほど散乱光強度が増えるというのも基本的には間違っていない考え方である)。 複数電子がある場合には、光の干渉という現象が起こるのだ。これは、高校物理で習ったことを思い出してほしい。図4は、2個の電子にX線が当たったときの簡単なモデルを示している。黒い矢印にそってやってくる波は入射X線、赤い矢印はとある方向への散乱X線を示している。入射X線の波を思い切って振幅が1のサイン波で表されるとしよう(ここでは
sinφとして、このときφはX線の波長に由来している。普通は複素数を用いた指数関数で表すのだが)。X線の光源はとても遠いので、平面波でやってくると仮定できる。つまり、電子1でも電子2でも同じ式で表される入射X線がぶつかっているのだ。で、入射X線に対して2θの方向に散乱された波は、弾性散乱を考えるので電子1で散乱されようが電子2で散乱されようが散乱波の波長は変わらないのだが、図4をみて分かるように「位相」がずれてしまう。そうすると、散乱波を単純に足し算をすると、位相のズレの分だけ強度が減衰してしまうのだ(図5)。 つまり散乱によって光路差が発生してしまうと、その位相ズレによって散乱合成波の振幅が位相ズレのない場合の散乱光強度に比べて小さくなってしまう。で、この光路差は何で決定されるかというと、散乱波と入射波のなす角(つまりθ)に由来している。だから、ディテクターの位置(2θ)によって強度が変化していくのだ。高校物理の教科書を見ればわかるが、これを干渉効果という。
★ここで気をつけてほしいのは、散乱振幅は確かに位相が半波長分ずれたら強度は0になってしまうのだが、それ以外のときには決してゼロにならないと言うこと。ブラッグの回折条件では、光路差そのものが僅かでも発生すると強度が0になってしまうように記述されているが、これは干渉効果に直接由来しているわけではないので注意。

複数の電子による散乱2(散乱基本式)
2つの電子による散乱波の合成を見てきて分かるように、その合成波の強度は干渉効果によって入射波と散乱波のなす角2θに依存することが分かった。更に、この考え方を、沢山の電子が分布しているサンプルにX線を当てた場合に一般化してみよう。 まず一般化のためには、さっき強調したように光路差について考えなくはいけない。で、光路差を考えるためには基準になる座標系が必要なのだ。電子の位置は相対的なものなので、適当に原点O(オー)を決めてあげればよい(どこをOにしても結果は同じ)。原点Oに対する電子の位置ベクトルをrとし、入射X線方向の単位ベクトルをs0、2θで散乱した波方向の単位ベクトルをsとしたとき光路差Δは、

となる。 ところで、量子力学がのたまうように、「電子がある位置に存在する」という考え方はちょっとナンセンスである。電子も波動という考え方によって空間全体にわたって分布しているのである。したがって、ある座標(位置ベクトル r)において、ある電子密度ρを定義したほうが分かりやすい。電子密度ρが大きいほどそれに比例して散乱は起こりやすくなると考えるのだ。
以上をまとめて電子密度分布をしたサンプルが散乱波を天下り式に書くと、

となるのだ。積分はサンプル全体の空間で発生する散乱波を積分して合成波にしている。また散乱波をサイン波ではなくて、数学的に使いやすい複素数を含む指数形式にしている。指数の肩には「X線波長に由来する項」と「(原点Oに対する)位相ズレの項」がかけ合わせてあるが、これは、指数なのでサイン式のカッコの中で足し算していることに対応している。(よく分からない人は複素関数の入門書を見てくだされ)
実は、この式は「とても一般化された式」なので、どんな材料でもOKなのである。非晶質だろうが、結晶だろうが、準結晶であろうが回折パターンが分かってしまう。 ところが、対象としている結晶性固体の場合、問題は位置rに対するρの値をアボガドロ数くらいの原子によって構成されたサンプ空間全体について知らないといけないい。それにその散乱波の式を積分しなくてはいけないのだ。。。。 これは、非常に大変であるのは察しが付くだろう。というか全く、非現実的で困ってしまうのだ。。。。
結晶のX線散乱現象
ってことで、この非現実的な散乱基本式をもっと現実的なところに持ってくるのが課題となる。で、察しがいい人は気づいているように、結晶の定義を利用すればいいのだ。結晶は比較的小さな単位の原子の並び(原子数個~数百個くらい)が周期的に並んでいる・・・だから、最小単位の格子だけ計算して、その結果を使ってうまくつなぎ合わせればいいのじゃないか?というアイデアを使うのである。この考え方はただしくて、次のようなストラテジーで回折パターンの基本式が出てくる。
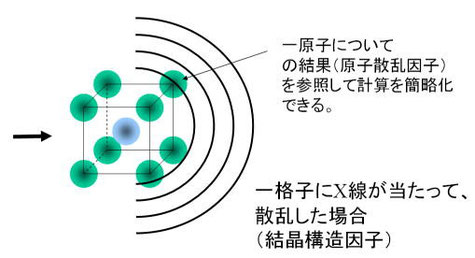
1.原子(またはイオン)が真空中に孤立して浮かんでいるとき、それにX線を当てたときの散乱現象を計算する。(図6)
2.その原子が何個か集まって、周期最小単位の一格子を形成したとき、それにX線を当てたときの散乱現象を計算する。(図7)
3.格子の並び方によって発生する散乱現象を計算する。(図8)
1.の結果得られるのが原子散乱因子であり、2.の結果が結晶散乱因子Fである。計算過程で、1.と2.はペアーとなっていて、1を計算してから2を計算する必要がある(注:★も参照)。3は1.2.に対しては独立していて、その式は後述するラウエ関数Lと呼ばれる。
この結果、粉末XRDで観測される回折強度は次のようになる。
(強度) = F(結晶構造因子) × L(ラウエ関数) × その他もろもろ
つまり、Fは一格子の中で原子(電子)がどのように並んでいるかを気にする関数であり Lは格子がどのように規則配列(格子の中身がどうなっていようがかまわない)するかを気にする関数なのであって、お互いに別々に計算してから、最後に両者を掛け合わせればOKというのが、回折現象の中身なのである。ちなみに原子散乱因子は結晶構造因子の関数に含まれていています。(後述)
あと、その他もろもろの中には、最初の方で説明した偏光因子なんかも入ってきますし、粉末法ではローレンツ因子(偏光因子とあわせてローレンツ偏光因子と呼ぶことが多い)などや吸収因子、温度因子、多重度なんかも入ってきますが、それは機会があったら説明することにする。
★もうお分かりだと思うが、結晶内での電子密度(←たとえば第一原理計算なんかでこのごろは簡単に計算できる)さえ分かれば、原子散乱因子を求めなくても全然かまわない。最もXRDパターンのシミュレーションを行なう限りにおいて、原子散乱因子→結晶構造因子を求める方法はとても高速だし、金属を含むような普通の無機結晶の場合パターンのシミュレーションに現れる誤差は極めて小さい。


原子散乱因子
ここでは、任意の原子やイオンが真空中に一個だけ孤立してプカプカ浮いている状態にX線が当たったときの事を考える。そうすると、何度も繰り返しになるけど球面波の散乱が発生する。ただし、原子の中には複数の電子がウロウロしているので干渉も起きる。ってことで、散乱基本式で説明した式をそのまま原子に当てはめればいいのだ。ただし積分範囲は、 Sample から Atom になる。

まず、式中の前指数項である電子密度ρ(r)だが、これはあらかじめ量子力学計算によって解かれた結果が各原子・イオンによってデータベース化してある。計算はかなり昔に誰かがきっと苦労して解いてくれたので、我々はそのデータベースを使えばいいということになる。その特徴なのだが、まず第一に電子数の大きい重元素ほど散乱強度は大きくなるということである。これは直感的にわかるだろう。ってことで、重元素と軽元素が含まれる系では、圧倒的に重原子由来の情報を回折法で拾ってしまうため、軽元素の解析は難しいのだ。もう一つの特徴は、一部の軽元素を除いて圧倒的に原子中央部に偏っているのだ。下の図は、第一原理計算で計算したとある重原子の電子密度分布なのだが、ほとんどの電子が中心付近に集中していることが分かるだろう。(ただし図は電子密度であり、電子数は体積との積なので注意が必要)。 いわゆる原子半径として教科書に載っているような領域では電子は希薄に存在するのみである。この領域の電子は価電子とよばれ、化学結合に重要な役割を果たすのだが、実際には非常に薄い電子雲を形成しているのである。一方非常に濃密に存在している内殻の電子というのは、原子やイオンで存在しようが、あるいは隣りの原子と共有結合とかを形成しようが、ほとんど分布に変化はない(化学結合とかにはほとんど寄与していない)。さて、原子散乱因子の式を見て直感的にわかるように、散乱波への寄与は電子密度がの寄与が大きいところだけ現れるから、XRDで観測される情報のほとんどは、実は内殻電子の情報なのだということになる。

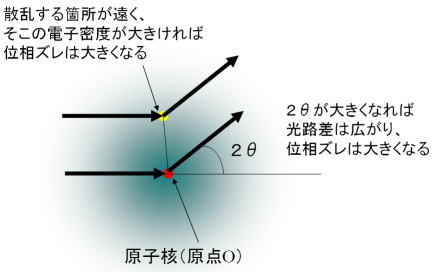
次に指数項となる位相ズレの問題について考えよう。ここでは基本的には位相ズレが大きくなればなるほど値は小さくなっていく(原子の常識的なサイズを考慮した場合)。では、位相ズレが大きくなる原因とはどういうときかということなのだが、それは光路差が大きくなるときであるので、散乱する方向が高角度側になるときと、散乱する電子が原点Oから離れているときがそれに該当する。(上図の右) まず2θの寄与から考えると、例えば2θが0のときは、どの電子にX線が入射して散乱しても光路差が現れることはない。つまり、原子散乱因子はその原子の持っている電子数に比例することになる。これは、さっき説明したように重原子ほど散乱が大きくなるということに対応している。(それから2θ=0のときにディテクターで観測するX線強度は散乱波のみならず(普通、圧倒的に大きい)透過波が含まれることに留意) で、2θが大きくなるほど光路差が大きくなるのでだんだんと散乱強度は小さくなっていく。このとき、2θが大きくなるにしたがって、内殻に近い電子よりも遠い電子(つまり価電子に近いほう)の方が、はげしく光路差を大きくしていく(上の図の右を見ればなんとなく分かるはず)。ってことで、2θが大きくなればなるほど、その散乱波に含まれる外側の電子の影響が激しく減少していくことになる。このことから、もし回折法で化学結合の状態(価電子の状態)を知りたいときは、低角側のピークの情報のほうが重要になってくるわけなのである。(昔は、価電子の分布を回折法で調べるということは、ほとんど装置の誤差範囲になるくらい困難(というか無理)な話だったのだが、最近は装置の発達のためなのか、解析法の発達のためなのか(中山にはよく分からない)、このような試みをよく聞くようになった。)
ということで、原子やイオンの種類というのは、たかだか(?)100~200種類程度なので、その結果をあらかじめテーブルにしてしまえばいいということは、さっき説明した。で、その結果はたとえば
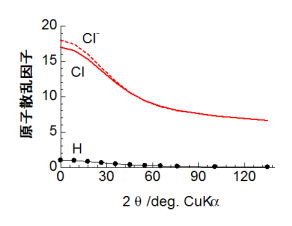
化学便覧とかにのかっていて、いつでも参照することができる。幾つか、例をみてみよう。 下の図は、水素、塩素、塩化物イオンの原子散乱因子を回折角(sinθ/λ となっているが、λは入射X線の波長っす)に対してプロットしたものだ。図から分かるように、回折角が0の時に電子数に一致するような値になっている。で、圧倒的に水素に比べて塩素の法が散乱因子が大きいことがわかるだろう。ってことで、重元素が含まれる系のなかで水素の寄与を見つけるのが難しいのは、図から分かりやすいと思う。では塩素と塩化物イオンの違いなのだが、塩化物イオンでは最外殻に電子が一個増えている状況であり、両者とも内殻の構造はほとんど変わらない。原子散乱因子を見ると、低角側で一電子分の寄与により散乱強度が変わっているのが見て取れよう。しかし、高角になるに従って、さっき説明したように外殻電子からの散乱の寄与があっという間になくなっていくので、結局塩素も塩化物イオンもほとんど区別がつかなくなるようになる。ところで、銅のターゲットを用いた実験室系のXRDの場合は、下の右図に示すように中性原子(Cl)とイオン(Cl-)における原子散乱因子の違いは20°以下で僅かにみられる程度であり、更に装置の特性上低角のデータには誤差が含まれやすい(というのは、僕のHPの別のところに書いてある)。ってことで、イオンの価数状態だとか共有結合性ウンヌンなどのような価電子の状態を反映したデータをXRD測定によってゲットするのは、直感的に言ってしまうとかなり厳しいのだ(と思う)。

結晶構造因子(その1)
つづいて考えなければならないことは「最小ユニット(単位格子のこと)で配列する原子の一団によって散乱したX線線がどのように干渉をするのか?」ということである。このような計算の結果が結晶構造因子と呼ばれており、とりあえず下図の"Fcryst = なんとか"という式で表わされる。散乱基本式と比べると見た目にはあまり変化していないが、実際上の計算量が大幅に減らされているので有用なのだ。 なぜ計算量が減っているのかというと、「積分」記号が「シグマ」記号になっていることである。もともと、散乱基本式では対象となる空間(この場合、格子内全体)の電子密度分布に対してX線の散乱波を足し合わせていく必要があるため積分式で表記されていた。しかし、結晶構造因子の計算では格子中の電子密度の空間的広がりをそのまま扱うのではなく、先にデータベース化されているとした原子散乱因子を使う。つまり、格子内に存在する原子一個一個について、「散乱光の強度が角度θに対してどのように発せられるか?= fj (θ)」という情報は既知なので、格子内にある原子核一点で散乱される干渉(これは高々数個~数十個?の原子核から発せられる散乱波を足し合わせるだけ)を計算すればいい。 なお原子核の位置(座標)の情報は、それぞれの原子から発せられる散乱波の位相のズレ(ベクトルrjとして表記される)に反映されている。位相のズレがずれるほど、回折強度が減ることは図5で述べたとおりである。したがって、格子の中で原子がどのように配列しているかという情報は、基本的に回折強度と関係している。時々、勘違いでピークの回折角と勘違いする向きもあるが、そういうこととは関係ないのだ。 最後に、結晶構造因子の計算(その1)についてもう一言。ここでは、格子内の電子密度分布を原子軌道に由来するそれ(つまり真空中に原子が一つだけプカプカ浮いているときの電子密度)を単純に足し合わせるような概念で、結晶構造因子の計算を端折っているわけだが、それでは化学結合による影響を反映してないではないか?といわれるとその通り。しかし、化学結合の形成は最外殻軌道をめぐる価電子の影響だけなので、基本的に内殻の電子密度にはほとんど変更がない。結果として、最外殻電子の影響が強い低角側のピークの強度に僅かに影響するだけで、基本的にX線の回折強度は化学結合を考慮しようがしまいがほとんど関係ないのである。むしろ、熱振動などにより原子核自体が揺籃する効果の方が、X線の回折強度には大きな影響が与えられる。熱振動のように、原子全体が動く場合には、低角よりも高角側で回折強度の低減がみられるが、それは機会があったら説明することにする。

ラウエ関数
結晶構造因子の計算では、単位格子一個に含まれる電子密度によって散乱・干渉するX線の計算をしたことになる。なので、図8で述べた手順に従って、最後に結晶の周期性を利用して、無限大個(あるいは約アボガドロ数個)の規則正しく並んだ単位格子から発生する散乱波の総和を得る。したがって、結晶構造因子Fcrystを使って、

と表わされる。ここで、X線の散乱を(結晶構造因子の算出で述べたように)全空間に対して積分する必要はなく、各格子点だけ計算すればよい。そこで、格子の集合体を図13のように考える。

図中、ベクトルRは格子点の位置を表わす。Rだけでは数値計算がしにくいので、単位格子の単位格子のベクトルa, b, cを用いて、R=
la+mb+ncと表わすと見通しが良くなる。(l,m,n)は図から直感的にわかるように 0~ L, M, Nの間の正の整数値となる。
したがって、散乱波はベクトルRの代わりに、a, b, cを使って、

となる。ここで、散乱波の入射および散乱の波動ベクトル(s0とs)/λも、計算をしやすくするようなベクトル表記を考える。どんなベクトル表記でも3次元空間上の全てをカバーするような座標系を設定すればいいので、Rを表記したように
(s0とs)/λ=px+qy+rzと表わしても構わない(注:ただしベクトルの単位はÅからÅ-1にする、あと波動ベクトルは別に小数になっても構わないことに注意)。
しかし、x, y, zを適当に選んでしまうと、位相ずれの計算(つまり指数関数の中身の計算)をする際に、
(la+ mb + nc)・(px +
qy + rz) = (lp a・x + lq a・y +
......)
となり、合計9項からなる面倒な式になる。 そこで、x, y, zのベクトルの取り方を下記のルールに従うように工夫すると…
a・x = 1 a・y = 0 a・z = 0
b・x = 0 b・y = 1 b・z = 0
c・x = 0 c・y = 0 c・z = 1
(la+ mb + nc)・(px +
qy + rz) = lp + mq + nr
となり、式がとても簡単になる。この時のベクトル、 x, y, z
を高名な逆格子ベクトル a*, b*, c*という。
上の式をみてわかるように、逆格子の定義 a と b*, c*は直行する、
aとa*の内積は長さ1となる(注:2πとする定義もあるので注意)などの教科書に書いてある条件が出てくる。 このように逆格子ベクトルは、(今のところ)波動ベクトル(の差)と実格子ベクトルの内積計算が簡単になるような座標系を設定しているということに注意されたい。なお、l, m, nは正数なので、p, q,
rの数値が整数のときには、散乱波の位相ズレが起こらないということに注意されたい。
さて、この条件を散乱波の式に改めて代入すると、

となる。 実は Σ exp(~) という式は、数学でいうところの等比級数の式にあたり、Eの2乗(つまり回折強度)は三角関数でΣ記号をはずした形式に表わすことができる。

このように表わされた関数をラウエ関数という。
さて、ここまで、式変形ができれば解析的に数値計算ができるのでXRDのパターンを計算することができる。・・・が、もう少し式について考察してみよう。
L, M, Nは格子の数なので、当然自然数である。一方逆格子ベクトルの係数、 p, q, rは別に整数にならなければならないという拘束条件はなかった。p, q,
rは入射波と散乱波のベクトル差である(s0-s)を決定する係数するので、回折角を表わす係数であるともいえる(注:この時点ではまだ回折現象とは言えないのであるが・・・)。したがって、X線の回折強度を与える回折角は連続的な数値(ブラッグの回折条件のように、離散的な値ではないということ)になっても、特に問題はないはずである。しかし、グラフソフトで
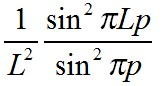
という計算をすると、下のような図になる。

図をみてわかるように、もし格子が一個(L=1)しかなければ(あたりまえだけど)、(Fcryst)2がそのまま回折強度となるのだが、格子の数が増えていくにつれて(L=2, 5,
10...)、pが整数のときだけ回折強度が現れ、それ以外の数値では回折強度がゼロになってしまう。実際に、格子定数が4Åの結晶について粒子サイズが1マイクロメートルくらいあることを想定すると、一辺に2500個程度の格子が並んでいることになるため、p, q, rが整数のときに
L2×M2×N2の値をとり、それ以外ではゼロとなるようなデルタ関数的な性質を示すことが、簡単に想像できる。
ということで、察しがついたかと思われるが、格子点が周期的に並ぶことで初めて逆格子ベクトルの係数が整数値のときのみ強度を持った回折現象が起こるというパターンが得られる。これは、ブラッグの回折条件の別の表現である。あるいは、散乱基本式において位相のずれが僅かでも生じると回折強度がゼロになるということが示されている。
結晶構造因子(2)とラウエ関数(2)
ラウエ関数の項目の最後で説明したように、今後の計算では(s0-s)/λ に対応する p, q, rのセットのうち整数のペアーだけ計算すればいい。これによって、計算量は大幅に低減する。そこで、整数のp, q, rのセットを今後は h,
k, l と表記する。記号の設定で気づいたと思うのだけど、 h, k, l はミラー指数に対応する整数セットであり、それについては別の機会でもう少し詳しく説明する。
なので、結晶構造因子も、もうちょっと簡略化ができて、
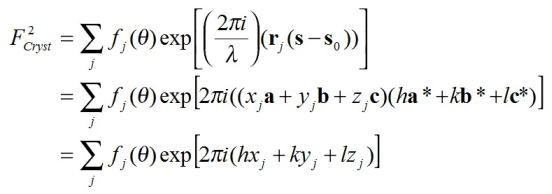
と表わされる。ここで、x, y, zは原子の分率座標を示している。 (なぜなら、r = xa + yb +
zc)
この変更の意味は、連続的な数値であった回折角θのうち、h, k, lが整数となる箇所だけ計算すればよいということを示している。
さて、ここまで来ると、散乱基本式を素直に適用するとベラボウな計算を強いられてしまった非現実的な回折強度の計算も、
1) 空間全体のrについて散乱基本式を解く必要はなく、
原子散乱因子のデータベースを用いて原子核の位置についてだけ計算すればよい
2) 格子の周期性から、h, k, lが整数の時だけ計算すればいい。
という計算の簡略化で、手計算でも頑張れば、あるいは最近のコンピューターを使えばほぼ(体感速度で)一瞬にして、計算が可能となることがわかる。
。。。。。
まだまだ、書かなければならないことはあるけど、疲れたのでまた今度。(つづく保証は?)
 Masanobu NAKAYAMA
Masanobu NAKAYAMA