第一原理バンド計算(基礎編)
基礎編では、第一原理計算を実際する人のために入力パラメータの簡単な理論的背景や計算の分類についてを説明する。
(更新履歴)
2004年10月5日にできたところまで公開
まだまだ未完成
2004年11月7日、一区切り
(用語)
(2004/10/5)
・第一原理(英語はfirst-principlesまたはab initio(英語ではない))とは、なんら実験データや経験パラメーターを使わないで理論計算をする方法の総称。でも、この業界では電子状態計算、平たく言うとシュレディンガー方程式を解く計算のことを暗に指すことが多い。したがって、このページも電子状態計算のお話となる。
・電荷密度(電子密度)ρは波動関数ψのノルムである。ノルムとは単純に言うと2乗ということ。
ρ(r)=|ψ(r)|2
概要
(2004/10/7)
第一原理と一口に言っても、近似法などで手法は沢山あるし、入力しないといけないパラメータも現実には複数ある。下の図はシュレディンガー方程式を概観したもの。これらの入力パラメータについて理解することを目標とするが、いつこのページが完成するかは不明。ちなみ、下の図はかなり結晶のバンド計算を意識したものなのでGaussianやガメスユーザーとかは注意すること。MOPAC(これは第一原理ではないし・・・・)に至ってはなぜか使ったことはあるけど、中山は完全に無知なのでこのページは全く役に立たないと思われる。
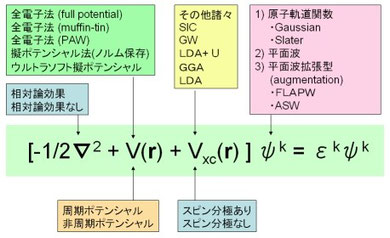
EXACT多体シュレディンガー方程式→ボルン・オッペンハイマー近似
多数の原子核・電子からなる系のシュレディンガー方程式のハミルトニアンのexactな形式は、

である。第一項と二項は原子核iと電子iの運動エネルギー、第三項は原子核-電子のクーロン相互作用、第四項は電子iとjのクーロン相互作用、第五項は原子核iとjのクーロン相互作用。 式からお分かりのように、ポテンシャルはクーロン力だけを考えている。スピンの交換相互作用とかも全部クーロン力に由来する相互作用となる。
ポテンシャルなのだが、電子や原子核の位置の関数になっている。しかし、正確な電子や原子核の位置を知るためには波動関数を知らないといけない。そんなわけで、次に述べるSCF法を使って計算をする。
その前にできることをすると言うことで、ボルンオッペンハイマー近似をする。陽子・中性子は電子の1840倍重いから動かないだろうと言う近似で、感覚的にも合理的だしわりと一致する。そうすると、Rの項は定数化するので、第一項はゼロになるし最終項は定数になる。そんなわけで、

となる。第一項は電子の運動エネルギー、第二項は電子-電子のポテンシャルで、これは系の形式に関わらずいつも同じである。(universalという)、Vextだけが、系の特徴(どこに原子があるか?)を反映するポテンシャルとなる。
ボルン・オッペンハイマー近似はほとんど全ての第一原理計算ソフトで採用されていると思われるが、化学反応や軽元素のように核子の運動に電子がついてこれない場合もでてくるので気をつけないといけない。また、これで分るように第一原理計算で求められるエネルギーは電子のエネルギーということになる。
★このシュレディンガー方程式は時間依存の部分を変数分離しているもの。時間依存の項が知りたい場合(たとえばある種の遷移など)は無力である。ソフトウェアーによっては対応しているものもあると聞くが、これは専門家レベルでチューンアップされたものと理解している。一般人にはまだまだ利用するのは難しいのではなかろうか?
☆運動エネルギー部分は相対論効果とよばれる効果を入れるか入れないかという選択がある。全電子法で重元素の場合は内殻の運動エネルギーが激烈に大きくなるから、相対論効果を入れないと現実に整合してこなくなるということだと理解している。とにかく、重元素は相対論効果を考えろということは間違ってないであろう。ちなみにDirac方程式をつかえと言うことは相対論を考えろと言うことの同義語である(と思う)。相対論効果を厳密に取り扱うのは難しいらしい、したがって適当なところで折り合いをつけたセミ相対論効果という近似法?を一般的なソフトでは採用しているようである。中山の経験では相対論を選択しようが非相対論を選択しようが計算時間があまり変わらないので、軽元素だろうが相対論を選択している。
★相対論についての追加コメント。MITの友達(彼は本当に頭がいい)によれば、相対論効果によってスピン量子数は自然に説明されるそうだ。つまりスピン量子数は自然の基本原理ではなく導かれるものらしい。もっとも、ランチのときの話なので厳密な話かどうかは不明。
★ボルンオッペンハイマー近似の表式から分るように、ポテンシャルはクーロン力だけを考えている。だから、同位体効果を考えるのは無理。水素も重水素も区別できない。ただし、第一原理分子動力学法(カー・パリネロ法)では答えは変わってくるであろう・・・。やったことが無いのでよく分らないけど。
SCF:シュレディンガー方程式をどうやって解くのか?
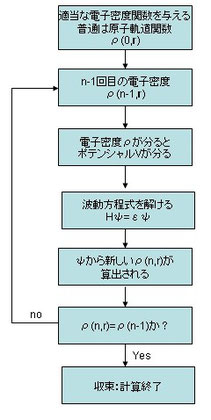
(2004/10/5)
シュレディンガー方程式の厳密解は水素原子のときだけ解ける、つまり他は解けないから近似解を求めることになる。近似法は学部の教科書に沢山載っているわけだけど、イマイチ具体的にどうやって解くのかが分りにくい。結局、
∇ψ+Vψ=εψ
を解けばいいのだが、問題はポテンシャルVが波動関数ψの関数だということ・・・。これは、電子の分布が変化すると、当然ポテンシャルも影響を受けるためである。
したがって、Vを知るためにはψを知らないといけないし、ψが知りたかったらVを知らないといけないという循環論になってしまう。第一原理計算のプロセスでは、だったら循環論で解いてしまえと言うことでSCF(セルフ・コンシステント・フィールド、自己無撞着)と呼ばれる方法で計算をする。
SCFでは、最初に答えに近いと思われる適当なψ(普通は原子軌道関数)を与えて、ポテンシャルやエネルギーを計算する。今度は、得られたポテンシャルで波動関数ψを計算する。これを繰り返していくと、いつか値があまり変わらなくなってくる。適当な基準で、計算を終了したときのψとエネルギーで計算結果とするのが、現在のほとんどのアルゴリズムの骨格になっている。もちろん、色々工夫をしているので、上述のように単純ではない。
右のスキーム図は上で述べたことをまとめただけ。
このサイクル一回をイタレーションとのたまう。また、最後のクライテリアでOKがでると収束するという。
この場合は密度汎関数法のスキーム例なので、ρを引き合いにしてイタレーションをしている。最後の収束条件は別にρじゃなくてもいいわけで、系のトータルエネルギーが落ち着いたり、イオンに働く力が落ち着いたりしただけでもよしとする。
☆:実際のSCFでイタレーション毎にできる新しいρ(n,r)をそのまま次のイタレーションに使うわけではない。古いρと新しいρを適当に混ぜて折り合いをつけている。この新しいρの割り合いを小さくすると、時間がかかるが正確になる。
基底関数
(2004/10/5)
シュレディンガー方程式を解くということは、波動関数ψを求めるわけだけど、関数形が全くunknownというのはSCFで解く場合かなり厳しい・・・というか現実的に無理。なので適当な鋳型になる関数を与える。この鋳型になる関数(たとえば、ガウシアンでもローレンチアンでもルジャンドルでも、なんでもいい)を基底関数という。突拍子もない関数形でも沢山足し合わせれば、波動関数ψを再現すると思われるのだけど、計算プロセスを少なくしたいから実際には限られた関数を使うわけで、例えばLCAO法は原子軌道を基底関数にしているわけだし、Gaussianというソフトではガウシアンを基底関数に使っているし、周期境界条件を備えたDFTプログラムの多くは平面波を基底関数にしている(というか、これは必要条件なんだけど(→参考 ブロッホの定理)。
波動関数に関する二つの考え方→ブロッホの定理→平面波基底関数
大胆に言えば、物理屋と化け屋は学部の基礎教養の時点で、分子や結晶中での波動関数についての記述の仕方が大きく違っている。化け屋は原子軌道を基底関数にしてLCAOで分子軌道を構築する。その便法としてHF法とかがあり、HF法などを使うソフトウェアーは、量子化学計算とくくられることもある。この場合、波動関数のサインが重要で、同じ符号なら結合性軌道になるし、異符号だと反結合性軌道ということになる。LCAO法やそれに似た方法は分子の結合を考えるときに直感的に分り易いので有利で、代表的なソフトウェアーにGaussianやガメス(ゲイモス?)というソフトがある(この文章を書いている時点で中山は使ったことがない)。実際に、LCAOを使うと波動関数を記述するために必要な関数の数が激減するので便利である。(最初から答えに近い関数を使えば当然と言えば当然なのだが)

しかし、結晶の場合にはLCAO法ライクなやり方には限界がある。なぜかと言うと結晶はある周期で無限に格子がつながっているので完全な記述にはアボガドロ数個の原子を計算しないといけないのだが当然そんな大量の計算をすることができない。これを解決する便法として、結晶からクラスターを切り出してきて計算をする方法などがある。切り口に当たる部分は結合が切れているので電子状態が大きく変化していて当てにならないので、中心部の電子構造だけを選択的にピックアップすると言う方法である。この方法は、系のトータルエネルギーを見積もれないし、本当に切り口の影響を受けてないのか?と不安が付きまとうジレンマがある。
そのジレンマに対する回答はブロッホ定理であり、周期性のある結晶の場合波動関数は次式であらわされるとした。

ここでTは並進ベクトル、kは波数ベクトルである。注意すべきは、ポテンシャルは結晶に対して並進対称性が成立・・・つまりTだけずらしたら全く同じである、のに対して波動関数はそうではなくて、平面波exp(ik)の変調を受けると言うことである。単純に言えば、この表式を使う限り単位胞だけ計算すれば、全ての格子を計算したことと同じことになる。そんなメリットがあるので平面波だけで波動関数を現すには沢山の関数が必要になってしまうが、結晶の計算では主流となっている。
第一原理計算でk点メッシュを入力せよと言うのは、上述の波数ベクトルkである。これは後で説明することにする。
★現在では単純なバルク(完全結晶)の計算よりも、むしろ不純物をドープした場合や表面のように切断された切り口の問題を扱うことが多々ある。この場合周期性が途絶してしまうので工夫が必要。工夫といっても、単に格子を大きくしていることが一般的なやり方。
★個人的には物理屋の電子の運動に対する考え方は化け屋のそれとかなり異なると思う。化け屋が原子軌道の線形和のような考え方をするのに対し、物理屋は金属の自由電子モデルから出発する。ドルーデ・モデルでは箱の中の電子について単純に理想気体の状態方程式を当てはめて考える。その後でポテンシャルの概念を加えていって、ジェリウムモデル→ブロッホの定理と拡張される。なので、化け屋は一般的に平面波を基底関数にする思考法が飛躍しているように見えてしまうが、物理屋からすれば自然な流れなのかもしれない。
密度汎関数法(DFT)
(2004/10/5)
計算において物理量、たとえばエネルギーを算出する際にどんな汎関数(関数の関数)を使うかと言うことで場合わけされる。
1.波動関数を使うとき・・・伝統的なHF法や分子軌道法(MO)は波動関数ψが基本関数となる。つまり エネルギーE = E[ψ]
2.電子密度を使うとき・・・これが密度汎関数法にあたる。エネルギーE = E[ρ]
歴史的には、ホーヘンベルグとコーンが理論的に確立・その後コーンとシャムが一電子方程式での解法を示した。(コーン・シャム方程式)
なんでDFTを使うのかというと、中山は多体問題を解くための実用的な一法であるからと認識している。
先に述べたボルンオッペンハイマー近似を使っても、電子-電子間インターラクションは多体問題として残ってしまう・・・つまり、

小文字のrは電子の位置ベクトル。
コーン・シャムはDFTを使えば「多体問題」を「沢山の一電子問題」にすることが可能であることを示したので偉いのであって、その表式は下記の通り。
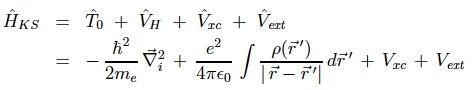
ここで電荷密度ρは、

したがって、ρであらわされたコーン・シャム方程式を使えば、N個の一電子問題になるわけである。
つまり波動関数を基底にするHF法では3次元空間内の電子N個の系の波動関数は各電子について3個、合計で3N個の座標関数に依存する関数となってしまう。一方、電子密度は電子が何個になろうとも3個の座標関数に依存するだけになる。
ところで、コーン・シャム方程式には問題があって、電子交換と電子相関に由来するポテンシャルVXC(交換相互作用ポテンシャル)の厳密な表式が与えられていない。この項は、本質的に電子と電子の相互作用や、自分自身の電子との相互作用もあり難しい。色々な近似法が提案されており、これがLDAとかGGAとか言われるポテンシャルになる。交換相互作用ポテンシャルについては後で述べる。
交換相互作用ポテンシャル
(2004/10/7)
コーンとシャムによって唯一具体的な表式を与えられていない部分である交換相互作用は、実は多体効果である。ということは、全然多体問題の解決をしていないのではと思う人もいると思われるが、実際に中山も同感である。
まず「交換」と「相関」の物理的意味は別々である。
「交換」は核A, Bの結合を考えた場合に表れる。全エネルギーは波動関数AとBの電子のエネルギーを単純なクーロン積分(つまり、<φ(A)|H|φ(A)>だけではなく「交換」項も加わる。これはAとBの電子を交換したときに結合性の場合は安定の方向へ、反結合性の場合は不安定の方向へ補正するエネルギーを与える。数式では<φ(A)|φ(B)>なる形式で表れるのでこれ以上の物理的な意味づけは今の中山には無理。これは、学部の物理化学の教科書に書いてある。(この文章を書いている時点で日本語の教科書を持ってないので間違っているかもしれない(注))
「相関」はもっと厄介でどうもぼやけた説明しかみたことがない・・・ので中山自身もよく分らない。色々、考えて下の図のような極端に単純なモデルではないかと推測している。つまり、2つの電子系で電子1が電子2に近づくと、電子2はクーロン反発で逃げ出してしまうと言う効果である。しかし、こんな古典的なモデルではないだろうと思うのだが・・・(不確定性原理とかを全く無視した見方だ・・・)。あるいは、モット・ハバードの概念による説明が分り易いと思う。これは、また別の機会に述べることにする。
なお、HF法ではどうかというとHF法は相関相互作用の項をそもそも記述していないので考えてすらいない。ポストHF法と呼ばれる手法で修正する。Xαポテンシャルとかがそれにあたると考えている。(ちなみに、Xαと書いてあるけど国内で普及しているDV-Xα法プログラムパッケージ(dvscat)はポストHF法ではない、ρで解いているから密度汎関数法なのだ。とてもややこしい。)
具体論に移る。多体問題ではあるが近似法はいくつかあり、これが論文でよく出てくるLDA、GGA、LDA+U、GW・・・その他諸々と言うことになる。またガウシアンとかではB3LYPとかがそれにあたると聞いている。中山は、LDA・GGA・LDA+U(GGA+U)について使用経験があるのでそれだけ述べる。というか他は無理。

LDA・・・多体問題を一体問題にするために、注目する電子に対して他の電子は電子密度平均として与えてしまうと言う方法。経験的にわりと現実を反映する(つまり計算と実験がよくあうと言うこと)ので多々用いられてきた。しかし、平均化した電子密度を使うので注目する電子自身との相互作用を計算してしまうなどの問題がある。また、電子・電子の相互作用が大きくなってくると計算結果がずれてくる。上の図は、中山の頭の中の非常に大雑把なイメージ。
GGA・・・LDAで取り扱った平均化した電子密度にグラディエントを更に考慮したもの。方法は考案者により多数ある。PW91, PBE,
B3LYPなどがある。この方法は、局在化した電子の系での計算に改善が見られる。
LDA+U・・・オン・サイト・クーロン効果であるハバードのUを使って局在化した電子の問題に対応した近似法。
☆以上、色々と記述したが、重要なのは LDA+U ⊇ GGA ⊇ LDA と考えてはいけないこと。新しいものが常にえらいと言うわけではない。。。。電子が局在化しやすい系はLDA+Uの方が、そうでもない時は(非局在の系では)LDAの方がよいことがある。
では、どうやって判断するのか?中山の知る限りこれという方法はない・・・。実験値に近いやつを選んでくれと言うのが本音だし、実際LDA・GGA・LDA+Uを計算して実験と比較した論文がPRBのような高級誌(一度掲載されたいものだ・・・)にでてくる。なんだか、第一原理の本質的な意味が薄れてくるようだけど、多体問題だから仕方ない。ちなみに、一番偉い(=新しい)?と思われているLDA+UなんかのUは試行錯誤パラメーターだったりする。(もはや第一原理ではない。)
☆あまりにも悲観的な書き方なので、もう少し議論しよう。非局在化した電子の系と言うのは、金属的な系のことを指す。だから、金属は一般的にLDAで計算するとよく一致する(GGAの方がいいときもある)。Siやガリヒソのような化合物半導体はよく知らない。硫化物もLDAかGGAでよく一致するように思える。最近電子産業で重要な酸化物だが、酸化物は一般的に局在化した電子の系なのでGGA以上が望まれる(それでもLDAの方があうこともあるらしい)。中山はまだまだ第一原理計算の経験が浅いが、実験や計算を通しておそらくほとんどの系はLDA+Uをしないといけないのだろうと思うようになってきた。
☆GGAの場合、格子サイズが大きくなる傾向がある。これは軌道同士が反発しているためか?一方LDAの場合は軌道同士が重なり易いためか格子サイズが小さくなる傾向がある。(→構造緩和の話を参照)
☆LDA+UのUは先ほど述べたように経験パラメーターである。しかし、中山の少ない経験によれば、パラメーターを1eVずらしたところで大きく結果が変わるようにも思えない。(注:トータルエネルギーは変わる、DOSとか電子密度に変化があまりないということ)。酸化物の場合4-5eVくらいが相場である。同じ化合物や元素でUを使った文献があれば参考にしたほうがいい。
★LDA+UのUを第一原理的に求めることも可能らしい。なんでも線形応答理論を使うとのこと。資料は持っているけど、数式だらけなのでおサルな中山には理解不能。
☆二つ以上の化合物の計算結果(特にトータルエネルギー)を比較する際に、片方はLDA、片方はLDA+Uというようなことをしてはいけない。
☆局在する電子の系でLDAを適用するときの最大の問題点はバンドギャップが再現できないこと(過小評価する)。酸化物の場合LDA+Uで大分改善するらしいが、よほど自信がない限りはバンドギャップの絶対値を議論してはいけない。(バンドギャップの見積もり方については解析編を参照のこと)
★中山はLDA+Uは物理学者のオモチャだと思っていたので去年まで興味がなかった(というか多忙で手が回らなかった)。そんな中GGA計算と実験のコンビで論文を書いているときにLDA+Uの論文が立て続けに出てしまい、この系でGGAやったらあかんと論文で指摘されて泣く泣く計算結果を廃棄してしまった・・・・。なので改心してこの頃LDA+Uを使えるようになった(使えると理解するは別です)。
全電子法と擬ポテンシャル法
(2004/10/16)
<全電子法>
全電子法は、文字通り系内の全ての電子について計算を行う。だから重元素になるに従って非常に計算が遅くなる。
大きく次の3(4)つに分類される。
1)APW法、LAPW法、FLAPW法・・・・APWは「補強された平面波」という意味。ブロッホ定理のところで、周期境界条件を使う場合は平面波の重ねあわせで波動関数を表現するとしたが、実際にはフェルミエネルギー近傍の自由電子的な振る舞いをする価電子に当てはめる場合にはよいのだが、内殻電子の場合は平面波で近似するのが大変難しい(沢山の平面波を使う必要がある、なんとなくわかるよね?)。そこで原子核から適当な半径(伝統的にマッフィン-ティン半径という)を設定し、マッフィンティン半径内は平面波で変調させた球面調和関数で表す手法。式で表すと下のようになる。上は平面波で表された価電子の波動関数、下は球面調和関数で表された内殻電子の波動関数である。
LAPW、FLAPWに従って数学的テクニックを使っている。LAPWのLは線形化という意味で、線形化して計算上の負担を軽減したもの。FLAPWのFはフルポテンシャルという意味で球面調和的な内殻電子の関数に非球面的な効果を加えて、計算精度を向上させたもの。当然時間はかかるが、現在もっとも計算精度の高い手法の一つ。

☆この手法の場合、内殻電子と価電子をつなぐ境目の波動関数の記述が一つのキーポイントになる。内殻の波と価電子の波がうまく境界部分で一致しないと収束が難しい。中々、収束しないと感じたら適当にマッフィンティン半径をいじってみると案外うまく収束することがある。収束し易い半径とは何かという経験則などは無い、運・不運の問題。たった0.1Å変化させるとうまく動作することがある。
☆2つの物質のトータルエネルギーを比較する場合は、必ず両者のマッフィンティン半径を同じようにとること。
2)LMTO法・・・・Lは線形化、MTはマッフィンティン、Oは軌道を意味する。マッフィンティンとは球状関数のことで、軌道関数を球状の軌道の線形和で表してしまうという大胆な近似。中山がD2のときに試しに使用したことがあるがとにかく計算速度が速くメモリー使用量も少ない。精度はどこまで当てになるのかよく分らないが表式を考えるとすこし不安がある。結局FLAPW法も割合早く動作するようになったし、速度と精度をそこそこ求めるのなら擬ポテンシャルのほうが有利だと感じたので今のところ使ってない。
3)KKR法・・・・中山は名前しか知らない。無知。シュレディンガー方程式を解くというより、多重散乱方程式を解く方法のことを指すのか?
4)PAW法・・・・中山は現在これを使っているくせに中身をよく分っていない。友達に聞いたところ、下の図のような感じだということはわかった。全電子法に分類しているが、擬ポテンシャル法との合の子と言った感じか・・・・。計算速度は速く、かつ精度を全電子法程度にだせる。(→ 参照先)

<擬ポテンシャル法>
一方、擬ポテンシャル法は、一般に物質の化学的性質は外殻の価電子に由来するので、思い切って内核の計算は打っちゃってしまって、価電子だけ計算するというものである。どうやって計算するのかというと、あらかじめ孤立した原子の内殻電子について適当な全電子法プログラムで第一原理計算をし、内殻電子と原子核によって価電子に及ぼすポテンシャルを算出しておく。すべての元素毎にあらかじめテーブルを作っておけば、あとはそれを使って価電子の計算をすればよいというもの。計算は当然速い。
概念的には的を得ているようだが、擬ポテンシャルを作成する際に現実には色々難しい側面がある。一番の難題は、擬ポテンシャルそのものが、後で述べる交換相互ポテンシャル(これは多体効果に由来する)に影響されるということ。そのため、擬ポテンシャルは用いる交換相互作用ポテンシャル毎に作らないといけない。
具体的には内殻電子の複雑な波動関数(当然ポテンシャルも)を下記のように近似(?)してしまって(これをソフト化という)、価電子部分の波動関数とポテンシャルを正確に得るということ。
なお、内殻電子部分の効果を全電子法で計算する際、ノルム(電荷密度)を保存する方法(これが一般的な擬ポテンシャル法)と、ノルムを保存しないで更にソフト化したウルトラソフト擬ポテンシャル法がある。後者のほうが速い(これはカットオフエネルギー(後述)を大変小さくすることができるため)

k点メッシュの決め方
(2004/10/11)
平面波基底関数(ブロッホ・セオレム)のところで波数ベクトルkについて紹介した。kは、実は量子数に対応するものと考えてもよい。ブロッホ定理を考えた場合は、無限周期の固体における波動関数の足し合わせとして表現されるので、とりうるkの値は無限となる。したがって全ての量子状態を、つまり全てのkについて計算をするのは不可能である。そこで、幾つかの代表的な点についてサンプリングをして、その点だけを計算して後は適当につなげることにする。だから、k点の数が大きければ大きいほど計算量は増えていってしまうので(結晶のk空間は3次元だから、少しkメッシュを細かくすると3乗で増えていく!)、当然計算時間は大きく変化する。理想的には、なるたけ少ないkで要求する精度の結果を得ればよい。よく分らないから、べらぼうにkを大きくすればいいやと思うと、生産効率は一気に落ちるので気配りが必要である。
このk点メッシュの作成は結晶格子に深く関係している(ブロッホ定理は結晶の周期性に注目していることを思い出すこと)。一次元格子において、下の左の図に表されるように大きな周期を持つ格子と短い周期を持つ格子を考える。波数ベクトルは逆格子(この概念を説明するのが厄介だ・・・・だから、今度機会があったらね)上の点であらわされるので、実格子空間で長い周期をもつ格子では逆格子は短く、逆に実格子で短い周期であらわされる格子は長くなる。さて、下の右の図はk空間に対しエネルギーレベルEをプロットしたもので、ディスパージョン・ダイアグラムと言う。ブロッホは、波動方程式は1格子の中だけで解けばよいとしたから、逆格子の範囲だけでkを定義すればよい。それ以上のkの値を持つ波動関数は、逆格子点でちょうど折りたたまれることになる。だから、k点のサンプリング点数に関して言えば、実格子での周期が長い少ないkメッシュでも、多くのk点をサンプリングしたことになる。一方、シンプルな結晶の場合は逆格子が大きいので、相当量のk点をとらないといけない。


☆では、どのようにkを決めたらいいのだろうか?経験がないと、全く勘所が働かない。中山の少ない経験では大体4Å-1でメッシュを4区切りさせてはどうかと思う。実は、たいていの場合この程度では全然k点は足りない。それで、k点を適当にこの基準から増やしたり減らしたりして第一原理計算を行い、トータルエネルギーを各kについてプロットしていく。(その結果が下の図)。そしてtotal
energyが落ち着いたところが、適切なkの値であると言うことになる。注意したいのは、一旦落ち着いたかのように見えても、実はもっとkを増やすとぶれ始めることがあるので注意しないといけない。
☆k点メッシュは上でも述べたように3次元空間で表される。また、区切り数は整数。なので普通のプログラムはa,b,c軸にそって逆空間を分割するように要求してくる。このときメッシュ間隔が均等になるようにしたほうがよい。時々単にk点の総数を聞いてくる場合があるが、おそらくプログラム内部で自動的にメッシュを区切っていると思われる。立方晶で30とk点を指定しても立方根の整数をとるから3x3x3=27のメッシュで実際には区切られることになる。次のメッシュは4x4x4=64だから、30、40、50、60とkを変化させても収束を調べても、すべて27で計算している可能性があるので、見た目は全く同じ値を返すことに注意しないといけない。
☆中山の個人的な経験では系の対象性によって奇数や偶数の組み合わせで突然値が発散することがある。おそらく、Γ点を含まずに計算してしまったため(逆格子のなかで対象性の悪い点だけピックアップして計算をすると、あまり精度がよろしくないそうだ)。念のため傾向をチェックするとよい。
☆構造緩和を含める時は、格子サイズのk収束性も確かめたほうがよい。特に使用するkの数が小さい時は、格子のサイズが大きく変化する。
☆構造緩和でも述べるが、最初に少ないkサンプリング点数で第一原理をして構造緩和をさせてからkサンプリング点数を大きくして構造緩和をさせると、わりと早く終わることが多い。
☆kサンプリング点が1の時はガンマ点計算といって、計算に寄与する複素数の虚数項がキャンセルする。それを踏まえてプログラムを最適化すると、ほぼ半分の時間で計算が終わる。これは大きな格子の系で有効である。
☆電子の各k状態(量子状態)へどう詰めていくかという指定は重要である。一般にテトラへドロン法と呼ばれる方法が使われるが、これは金属では時間がかかってしまうし力がすこしおかしくなる。多少フェルミ準位近傍で電子のつめ方をブロードニングさせたほうがよい場合が多いとか(中山はあまり金属の計算をしたことがないので注意)。これは丁度、有限温度におけるフェルミ付近近傍の電子占有状態を考えるのに似ている。
☆構造緩和後はk点メッシュのとり方が、構造が変ったせいで非対称になることがある。精度の高い計算をする場合は、構造緩和終了後、再度1イタレーションさせたほうがよい。

カットオフエネルギーの決め方
(2004/10/12)
やはり平面波基底関数(ブロッホ・セオレム)の場合に関連する。
波動関数を色々な平面波の足し合わせで考えるとき、より複雑な形の波動関数を表現するためにはなるべく短い波長(つまり大きいエネルギー)の平面波を使うとよい。ということで、カットオフエネルギーは、どこまで短い波長の平面波を使うかに関連するパラメーターと言える。カットオフエネルギーを上げると、使用する波動関数の数が3/2乗に従って増えるので計算時間が大きく増加することに注意する(次式)。

☆それぞれのソフトで推奨される経験的な値を普通はマニュアル中(あるいはデフォルト設定として)与えているので、そのまま使えばいい場合が多いが、過剰に見積もっている場合が多いので多量の計算をする場合には最適化した方がいいかもしれない。
☆擬ポテンシャルプログラムの場合は、擬ポテンシャルファイル(つまり原子毎)に使用したカットオフエネルギーが書かれていることがある。用いる原子の中で、最大になるカットオフエネルギーを用いるか、精度を上げるには1.5倍程度の値を使うとよい。
スピン分極
(2004/11/7)
ご存知の通りスピンにはアップとダウンの2つの量子状態がある。フントの法則により同じ軌道に二つの電子が入るよりも、スピンがパラレルの状態で別の軌道に入っていったほうが安定になる。このスピンの分極をこれを再現するかしないかというのが、大概の第一原理計算のソフトには付いている。もちろんスピン分極を常に選んでおいたほうが安全ではあるのだが、アップとダウン2つの状態を計算するので、計算コストは2倍になる。典型元素の化合物や一部の遷移金属化合物の場合は、軌道は完全につまるか空であるので、スピン分極なしで計算をするとよい。
☆同一原子内のスピン分極効果は多体効果である。自由電子的な振る舞いの場合はLDAなどでも十分実験結果を再現するが、強相関系の場合はLDA+Uなどの方法が必要である。ちなみにUの値を大きくすると、究極的には高スピン状態になる。
☆原子-原子間のスピン間相互作用は、いわゆる強磁性(FM)・反強磁性効果(AFM)に相当する。理屈では、FM・AFMのどちらが安定かという問題はSCFで解けそうだが、とても弱い相互作用なので識別するのは難しい。またAFMの場合は、周期境界条件の関係上、大きなセルが必要な場合がある。したがって、先にスピン状態をFMやAFMとして与え、両者のトータルエネルギーを比較し、FM・AFMのどちらが安定かを決定する。FMでもAFMでも、普通はDOSやトータルの電荷密度分布に際立った変化はない。しかし、トータルエネルギーについては大きな変化が現れることがある。
構造緩和
(2005/7/10)
ボルン・オッペンハイマー近似の意味を考えると分るように、SCFの過程で原子核に関する計算はなんら行わない。なので「どの位置に原子核があるのか?」という問題について考えるのはナンセンスである。従って実験情報が要らないという第一原理であるにもかかわらず、結晶構造は計算者が先に与えなければならないという暗黙の了解がある。しかし、原子核位置についてある程度の補正は可能である。
先に述べたように、第一原理計算によってある原子構造における電子の密度分布を明らかにすることができる。このとき同時にポテンシャルの項も明らかになる。ポテンシャルが明らかになると、その勾配から原子核に働く力が簡単に計算できる。最適な構造は、各原子にとって一番、力がかからないと考えられる。そこで原子の位置を力の向きに沿って移動して、再度シュレディンガー方程式を解く(SCF)。この過程を繰り返して、エネルギー的に一番安定な原子配列を見つけることで、結晶構造の構造緩和ができる。
★現実には単純に力の大きさに比例配分して動かしているわけではなく、色々な工夫があるそうだ。
☆言い換えるとシュレディンガー方程式をSCFで解く過程に、さらに原子位置を最適化するループを加えたことになる。従って、計算量は膨大になるため、全電子法のような計算速度が遅い方法に適用することは難しい。通常は擬ポテンシャル法などで行う。
☆1ステップ毎に原子を移動させる方向は力のベクトルによって決まる。これは空間群に由来する。なので、どうやっても原子が移動できない場所が群論の拘束条件から出てくることもある。これを避けたい場合は、わざと一原子だけ特殊等価点などからずらして計算するとよい。(つまりP1空間群にしてしまう)。しかし、このような手法は通常計算時間を倍化させてしまう。
 Masanobu NAKAYAMA
Masanobu NAKAYAMA